백준 12015번 - 가장 긴 증가하는 부분 수열 2

가장 긴 증가하는 부분 수열 (백준 11053번)

개념 : LIS

난이도 :

링크 : LIS : https://www.acmicpc.net/problem/12015

---

최적화

만일 이전 글을 읽지 않았다면 읽고 오는 것을 추천한다.

배열 $A$

[9, 6, 9, 6, 1, 6, 9, 1]

$LIS(A[1 \dots i])$

[1, 1, 2, 1, 1, 2, 3, 1]

더욱 최적화해보자.

그래프를 인덱스와 수의 크기로 만드는 것이 아닌, $LIS(A[1 \dots n])$의 길이와 수의 크기로 만들어보자. 다음과 같아진다.

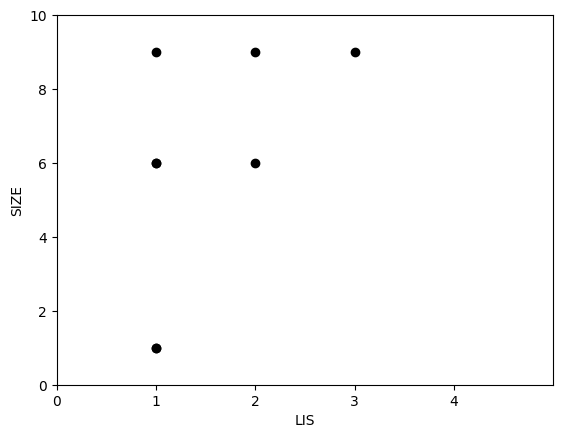
같은 $LIS$ 길이과 같은 수의 크기가 있을 수 있음에 유의하자. 여기에 크기가 7인 원소가 추가된다고 해보자.

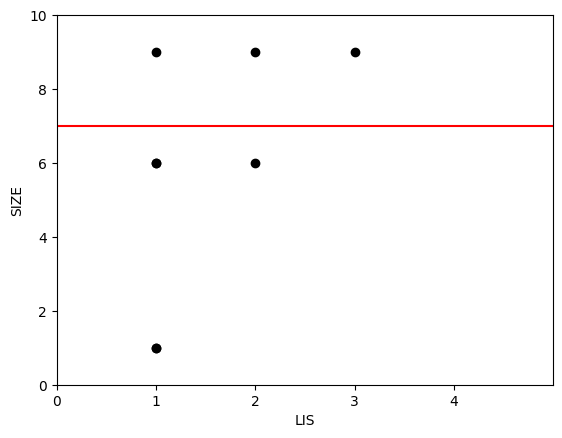
7미만의 원소 중 가장 $LIS$의 길이가 큰 값이 다음 $LIS$의 값이 된다. 여기서는 크기 6인 원소가 $LIS$의 길이가 2이므로 7의 $LIS$길이는 3이된다.

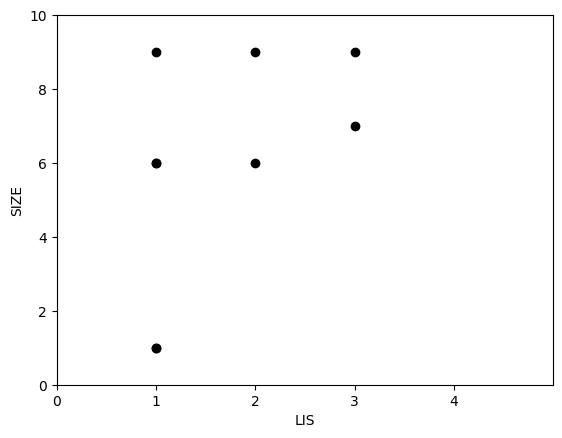
여기서 중요한 관찰이 나온다. 각 $LIS$별로 점이 여러개 있으나, 사실상 유효한 점은 크기가 가장 작은 점이다.

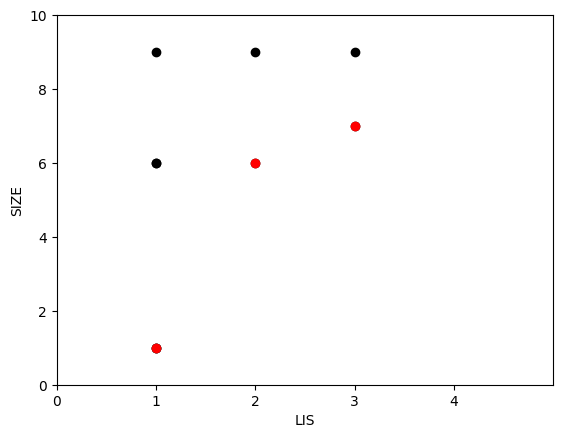
같은 방식으로 직선을 그어 가장 긴 $LIS$를 찾을 때에도, 검은점이 유효하다면 반드시 빨간점도 유효하다. 따라서 검은점을 지워도 상관이 없다. 그 뜻은 $LIS$별로 최솟값 1개의 값만 가지고 있어도 무관하다는 것을 의미하며 최적화의 중요한 관찰이 된다.

$DP$를 각 $LIS$에 저장된 값 중 가장 작은 값이라고 정의하면 점화식을 다음과 같이 만들 수 있다. (초기에는 모두 $\infty$ 값으로 초기화)

\[LIS(A[1 \dots i]) = min_{A[i] < DP[j]}(j) - 1\]

$LIS$의 길이는 $A[i] < DP[j]$를 만족하는 가장 작은 $j - 1$를 매번 찾아주면 된다.

\[k := min_{A[i] < DP[j]}(j)\] \[DP[k] = min(A[i], DP[k])\]

같은 $DP$에 속하게 되는 값들끼리는 최솟값만 남겨놓으면 족하다.그러면 $LIS \ 1$ 문제를 다음과 같이 해결할 수 있을 것이다.

#include <bits/stdc++.h>
#define MAX 1'010'101'010

using namespace std;

int dp[1010];
int n;

int main() {
    cin >> n;
    fill(dp, dp + n + 1, MAX);
    for (int i=0; i<n; ++i) {
        int x; cin >> x;
        int j=0;
        while (dp[j] < x) j++;
        dp[j] = x;
    }

    int ans = 0;
    while (dp[ans] != MAX) ans++;
    cout << ans;
}

하지만 생각해보면 $A[i] < DP[j]$를 만족하는 가장 작은 $j$를 찾는 과정은 어디서 많이 본 것 같지 않은가?

$lower\ bound$가 바로 그것이다. $DP$배열에서 $A[i]$의 $lower \ bound$ 위치를 찾고 넣어주면 된다. 이 과정이 $log(N)$으로 축소되므로, 전체 문제를 $O(NlogN)$에 해결할 수 있게 된다.

#include <bits/stdc++.h>
#define MAX 1'010'101'010

using namespace std;

int dp[1010];
int n;

int main() {
    cin >> n;
    fill(dp, dp + n + 1, MAX);
    for (int i=0; i<n; ++i) {
        int x; cin >> x;
        int j = lower_bound(dp, dp + n + 1, x) - dp;
        dp[j] = x;
    }

    int ans = 0;
    while (dp[ans] != MAX) ans++;
    cout << ans;
}

이렇게 $LIS$문제를 $O(NlogN)$에 해결할 수 있게 된다.