세그먼트 트리의 원리와 시간 복잡도

9 minute read

이전에 티스토리 블로그에 올려두었던 것들을 깃허브 블로그로 옮기고자 한다. 세그먼트 트리부터 펜윅 트리까지 작성해두었는데, 꽤 유익할 것이다. 모든 의사 코드는 파이썬의 문법을 모방하였다.

구간 합 구하기

배열이 있고, 특정 구간 $[l, r]$의 합을 구하는 쿼리를 빠르게 구하는 문제를 Range Sum Query(이하 RSQ)라고 표현한다. 이러한 고전 문제 중 쉬운 문제는 아래와 같다.

위 문제의 지문을 곧이 곧대로 구현하면 TLE(Time Limit Error)를 받게 된다.

for N = 1 to Q:
	i, j = input()
	print(sum(A[i:j]))

이 경우, 쿼리당 최대 100000번의 연산이 발생하므로, 발생할 수 있는 최대 연산의 수는 $O(N^2)$으로 대략 100억번의 연산을 수행해야한다. 대략 1초에 1억번의 연산을 한다고 했을 때, 100초의 시간이 걸린다. 이러한 문제를 해결하기 위해 누적합 (prefix sum)을 이용하여 미리 더해놓는다.

\[S[N] = \sum_{k=1}^{N} A[k]\]

그렇다면 $S[N]$를 위와 같이 정의하자.

\[S[j] = A[1] + A[2] + ... + A[i-1] + A[i] + ... + A[j-1] + A[j]\] \[S[i-1] = A[1] + A[2] + ... + A[i-1]\] \[S[j] - S[i-1] = S[i, j] = A[i] + .... + A[j]\]

이렇게 $S[j]$ 와 $S[i-1]$를 구할 수 있다. 아래는 이를 그림으로 표현한 것이다.

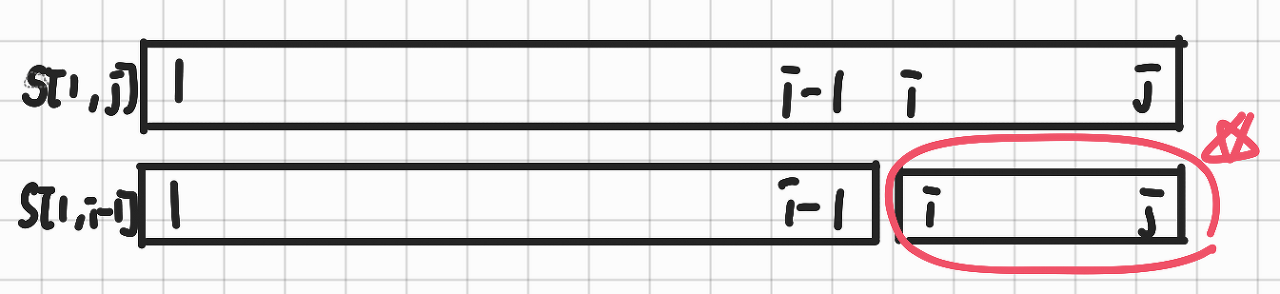
만약 $S[1] \dots S[N]$을 모두 전처리를 통해 알고 있다면, 단 한번의 뺄셈으로 답을 구할 수 있다. 즉, 한 번의 쿼리당 $O(1)$의 시간으로, 총 $O(N + Q)$의 구간 합 구하기 4 문제를 해결할 수 있다.

구간 합 구하기 5 역시 이를 응용해서 해결할 수 있다. $S[x , y]$를 $(1,1)$ 를 왼쪽 위 꼭짓점, $(x,y)$를 오른쪽 아래 꼭짓점으로 하는 정사각형의 누적합으로 정의하면, 포함 배제의 원리로 간단하게 해결할 수 있다.

세그먼트 트리(Segment Tree)

전처리(build)

이제부터 세그먼트 트리의 유용함에 대해 설파한다. 우선 아래의 문제를 읽고 오자.

구간 합 구하기

위 문제들과의 차이점이 뭔지 발견하였는가? 바로 업데이트가 있다. 중간의 있는 수들이 바뀌기 때문에 구간 합 구하기 4의 방식으로는 해결할 수 없는데, 하나의 숫자를 바꾸면 그 뒤쪽의 모든 누적합이 바뀌어야한다. 업데이트 쿼리 하나당 O(N)의 시간이 소요되어 TLE를 받게 된다.

세그먼트 트리는 이 업데이트 연산을 수행하기 위해, 구간을 쪼개어 구간마다 누적합을 구해놓는다. 구조를 눈으로 살펴보자.

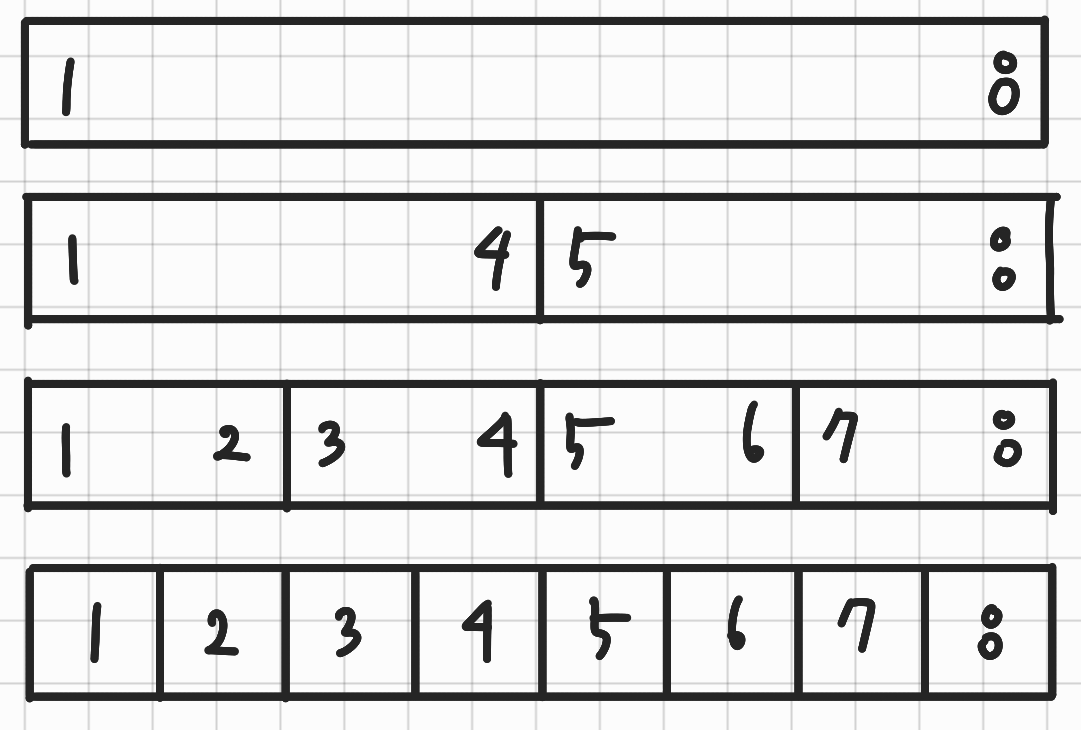
8개의 원소가 있는 A를 다음과 같이 쪼개어 각각의 칸에 누적합을 구해놓았다고 가정하자. 각 칸의 맨 왼쪽은 구간의 시작점, 맨 오른쪽은 구간의 끝점을 나타내는 것으로 [1 4]라고 하면 A[1] + A[2] + A[3] + A[4] 가 더해져 있는 것이다.

A = [ 1, 2, 3, 4, 5, 6, 7, 8 ]

그리고 이 배열로 위 그림에 누적합을 구하면 다음과 같다.

각 구간의 합을 위와 같이 구할 수 있다. 여기서 관찰할만한 점은 가장 아래 계층에서부터 이웃한 두 수를 더하며 루트까지 올라간다는 점이다. 이 점을 이용하여 전체 트리를 구성하게 된다. 이제 세그트리 구현을 위한 의사 코드를 살펴보자.

Class Node:
    int sum # 구간의 합
    int start, end # 구간의 왼쪽, 오른쪽 경계
    Node LEFT, RIGHT

각 노드의 설계도이다. 각 노드는 구간의 합, 구간의 왼쪽, 오른쪽값, 왼쪽, 오른쪽 노드의 참조를 갖는다. 이제 세그먼트 트리 전체를 재구성해보자.

def build(start : int, end : int) -> Node:
    # 해당하는 구간의 노드를 만들고, 해당 노드를 리턴
    new_node = Node()
    # 새로운 노드의 구간을 업데이트
    new_node.start = start
    new_node.end = end
    
    if start == end:
        # 구간에 포함된 값이 1개라면, 더 쪼갤 수 없으므로 재귀 종료
        return new_node

    # 중간을 기준으로 구간 쪼개기를 진행.
    mid = (start + end)/2
    new_node.LEFT = build(start, mid)
    # 왼쪽 자식을 재귀로 생성
    new_node.RIGHT = build(mid + 1, end)
    # 오른쪽 자식을 재귀로 생성

    # 자기 자신을 리턴하여, 부모 정점이 자식으로 삼도록 함
    return new_node

위 코드를 진행하면, 루트에서부터 구간을 절반씩 줄여가며 모든 리프노드까지 트리를 구성하게 된다. 만약 구간이 $[1, 8]$이라면 build(1, 8) 함으로써 초기화하는 것이 가능하다. 하지만 아직 아무런 값도 등록되어 있지 않은데, 리프노드에 값을 등록하고, 위 그림과 같이 리프노드에서부터 위쪽으로 올라가며 더할 수 있도록 구현을 추가하자.

def build(start : int, end : int) -> Node:
    # 해당하는 구간의 노드를 만들고, 해당 노드를 리턴
    new_node = Node()
    # 새로운 노드의 구간을 업데이트
    new_node.start = start
    new_node.end = end
    
    if start == end:
        # 리프노드이므로 구간의 유일한 값 arr[start]을 sum으로 등록한다. 
        new_node.sum = arr[start]
        return new_node

    # 중간을 기준으로 구간 쪼개기를 진행.
    mid = (start + end)/2
    new_node.LEFT = build(start, mid)
    # 왼쪽 자식을 재귀로 생성
    new_node.RIGHT = build(mid + 1, end)
    # 오른쪽 자식을 재귀로 생성

    # 자기 자신의 sum 값은 반드시 두 자식의 sum의 합
    new_node.sum = new_node.LEFT.sum + new_node.RIGHT.sum
    # 자기 자신을 리턴하여, 부모 정점이 자식으로 삼도록 함
    return new_node

위는 자주 사용하는 세그먼트 트리 빌드 패턴이다. 리프 노드일 때, 해당 구간의 값을 등록하고, 재귀가 끝나고 올라가는 길에 부모 정점에 값을 전달한다. 이것이 세그먼트 트리의 중요한 특징인데, 바로 부모 노드는 두 자식 노드의 결합으로써 이루어진다는 점이다. 이는 수많은 Range Query 문제를 해결하는데에 도움을 준다. 이제 업데이트에 대해 알아보자.

업데이트

만약 여기서 A[3] 에 4를 더하는 업데이트가 들어왔다고 하면 다음과 같다.

이 때 바뀌어야하는 값은 A[3]이 포함되어 있는 구간만 바뀌면 된다. 연산은 단 4번만 수행하면 되며, 이것은 트리의 높이에 해당하는 값이다. 루트에서부터 한 계층씩 내려가며 그 크기가 절반으로 줄어들기 때문에 높이는 $O(logN)$이 될 수 밖에 없다. 따라서 업데이트 연산은 $O(logN)$의 시간복잡도를 갖는다. 대략 배열의 크기가 1,000,000(백만) 이어도 대략 20번의 연산밖에 일어나지 않는다.

이제 업데이트 함수를 구현해보자.

def update(node : Node, idx : int, val : int) -> None:
    # 해당 노드를 update 하며, 리턴값은 없음
    if node.LEFT == node.RIGHT:
        # 마지막 계층 도달. 추가해주고 종료
        node.sum += val
        return
    mid = (node.LEFT + node.RIGHT) / 2
    if idx <= mid:
        update(node.LEFT, idx, val)
    else:
        update(node.RIGHT, idx, val)
    # 자식들의 update가 모두 끝났으므로 다시 자신의 값을 구함
    node.sum = node.LEFT.sum + node.RIGHT.sum

리프노드에 도달하여 값을 더하고, 다시 부모로 올라가는 과정에서 두 자식노드의 결합으로써 새롭게 값을 구성한다. 각 노드별로 더하기만해도 괜찮지만, 이렇게 하는데에는 이유가 있으니 넘어가기 바란다.

RSQ

구간의 합 쿼리를 수행하는 방법에 대해 알아보자. 중요한 것은 미리 계산해놓은 값들을 최대한 이용하는 것이다. 이해를 돕기 위해 2부터 7까지의 구간합을 최소의 노드로 구하는 상황을 눈으로 톺아보자.

위의 그림의 색칠된 부분을 모두 더하면 A[2] 부터 A[7] 까지의 모든 원소가 들어 있음을 확인할 수 있다. 2부터 8까지의 예시를 하나만 더 보자.

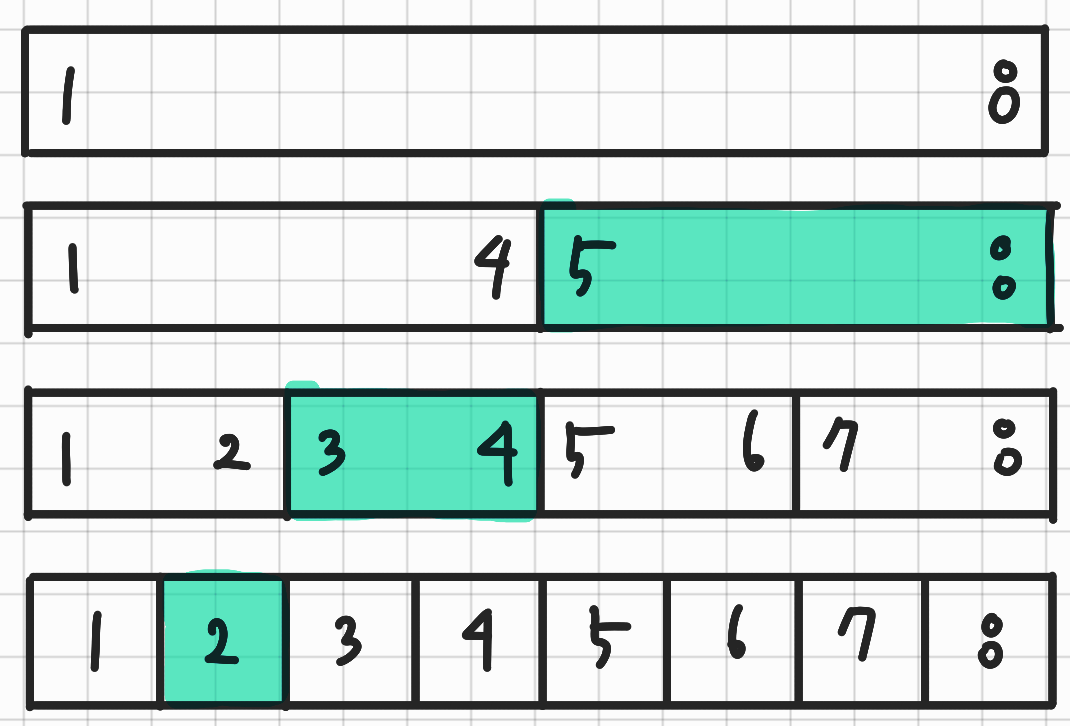
역시 A[2]부터 A[8]까지 모든 원소가 합해져 있음을 확인할 수 있다. 특징을 살펴보면 다음과 같은 사실을 관찰할 수 있다.

쿼리 구간에 완전히 포함되는 구간 중 가장 큰 구간을 선택

예를 들어 A[5]부터 A[8]까지의 합을 [5, 6] 구간 + [7, 8] 구간으로 구하지 않는다. 가장 적은 수의 연산을 하기 위해서이기도 하다. 이 연산 역시 $O(logN)$번의 연산으로 구할 수 있는데, 이 부분은 시간 복잡도를 분석할 때 살펴보자. 이제 구현을 위한 아이디어를 확인하자.

구간에 완전하게 포함되는 노드 중 가장 큰 것의 합들을 겹치지 않게 모아주기

여기서 2개의 키워드로 나눌 수 있는데 1. 완전하게 포함되는 2. 구간에 포함되는 노드 중 가장 큰 것이다. 첫 번째 키워드에 대해 이야기해보자.

만일 $[L, R]$ 구간의 합을 구한다고 한다면 완전히 포함되는 노드는 아래의 조건을 만족할 것이며

L <= node.LEFT and node.RIGHT <= R

완전하게 포함되지 않는 노드는 다음과 같은 조건을 만족할 것이다.

node.RIGHT < L or R < node.LEFT

완전하게 포함되는 노드는 정답에 포함시키면 될 것이며, 완전하게 포함되지 않는 노드는 거들떠보지 않아도 괜찮을 것이다. 마지막으로 위 두 조건에 걸리지 않은 노드는 조건에 애매하게 걸쳐있는 노드이다. 이 경우에는 왼쪽 오른쪽 자식들로 분할하여 같은 탐색을 재귀적으로 반복하면 될 것이다.

두 번째 키워드 구간에 포함되는 노드 중 가장 큰 것은 루트에서 시작하여 재귀적으로 내려가기 때문에 자연스럽게 해결된다. 항상 부모 노드를 먼저 만나며, 조건에 해당된다면 정답에 포함시키게 된다. 이 때 이 노드가 해당 구간에 포함되는 노드 중 가장 큰 노드이므로 더 이상 고려할 필요가 없다. 이제 함수를 설계해보자.

def query(node: Node, L: int, R: int) -> int:
    if node.RIGHT < L or R < node.LEFT:
        # 완전히 포함되지 않는 노드는 답에 영향을 주지 않기 위해 0을 리턴
        return 0
    if L <= node.LEFT and node.RIGHT <= R:
        # 완전히 포함되는 노드는 자신의 값을 리턴
        return node.sum
    # 위 두 조건에 걸리지 않았다면 애매하게 걸쳐 있는 노드, 자식들에게 맡기자.
    # 왼쪽 자식이 건져오는 값과 오른쪽 자식이 건져오는 값을 합함
    # 만약 포함되는게 없다면 0으로 리턴하여 아무런 영향이 없을것
    return query(node.LEFT, L, R) + query(node.RIGHT, L, R)

시간복잡도

우선 빌드하는데 걸리는 시간은 $O(N)$이다. 세그먼트 트리의 노드의 최대 개수는 엄밀하게 $N$보다 크거나 같은 가장 작은 2의 제곱수의 2배가 된다. 이 부분은 다음 포스팅에서 언급해보겠다. 그리고 업데이트에 걸리는 시간은 $O(logN)$이 됨을 이전 업데이트 부분에서 미리 언급한 바 있다.

중요한 것은 RSQ, 쿼리의 시간복잡도이다. if node.RIGHT < L or R < node.LEFT: 조건과 if L <= node.LEFT and node.RIGHT <= R: 조건에 걸리지 않는 노드의 개수가 중요하다. 즉, 애매하게 걸려있는 노드의 개수가 중요한 것이다. 이 때, 잘 생각만 해보면 매 재귀 깊이에서 최대 단 2개만이 나뉘는 것이 가능하다. L과 걸치는 노드 R과 걸치는 노드 최대 2개만 존재 가능하다. 따라서 매 재귀 단계마다 실제 만날 수 있는 노드의 최대 개수는, 0 재귀 깊이는 1, 1 재귀 깊이는 2, 그 이후로는 4개이다. 최대 재귀 깊이는 $O(logN)$이고, 각 깊이마다 만날 수 있는 노드의 개수가 상수이므로, 전체 쿼리 알고리즘의 시간복잡도는 $O(logN)$이 된다.

실제 구현

실제로 구현한 코드를 첨부한다.

python

arr = [*range(1, 257)]  # 1부터 256


class Node:
    def __init__(self, start, end) -> None:
        self.sum = 0                    # 구간의 합
        self.start = start              # 구간의 시작
        self.end = end                  # 구간의 끝
        self.left = self.right = None   # 왼쪽, 오른쪽 자식


class Segtree:
    def __init__(self) -> None:
        # 세그먼트 트리 [1, 256] 범위 생성자
        self.root = self.init(1, 256)
        # 트리의 루트 생성

    def init(self, start: int, end: int) -> Node:
        # 노드 생성
        node = Node(start, end)
        if start == end:
            # 마지막 계층 도달. 노드의 값 등록
            # 현재 세그먼트 트리는 1-based index이고
            # arr는 0-based index이므로 start에 1을 빼줌
            node.sum = arr[start-1]
            return node
        mid = (start + end)//2
        # 왼쪽, 오른쪽 자식들을 생성하고
        node.left = self.init(start, mid)
        node.right = self.init(mid+1, end)
        # 완성 이후 구간의 합을 줍줍
        node.sum = node.left.sum + node.right.sum
        return node

    def update(self, node: Node, idx: int, plus: int) -> None:
        # 노드를 업데이트
        # idx : 업데이트 하고자 하는 값
        # plus : 더하고자 하는 값
        if node.start == node.end:
            # 마지막 계층 도달. 노드의 값 추가
            node.sum += plus
            return

        mid = (node.start + node.end)//2
        # idx가 mid보다 작거나 같으면 왼쪽으로 아니면 오른쪽으로
        if idx <= mid:
            self.update(node.left, idx, plus)
        else:
            self.update(node.right, idx, plus)
        # 자식들 업데이트 완료. 구간합 줍줍
        node.sum = node.left.sum + node.right.sum

    def query(self, node: Node, l: int, r: int) -> int:
        # 구간합 구하기
        # l : 구간의 왼쪽 값, r : 구간의 오른쪽 값
        if node.end < l or r < node.start:
            return 0
        if l <= node.start and node.end <= r:
            return node.sum
        mid = (node.start + node.end)//2
        return self.query(node.left, l, r) + self.query(node.right, l, r)


tree = Segtree()

print(tree.query(tree.root, 2, 5))          # 2+3+4+5
tree.update(tree.root, 3, 2)                # 3 -> 5
print(tree.query(tree.root, 2, 5))          # 2+5+4+5

#include <bits/stdc++.h>

using ll = long long;
using namespace std;

struct Node
{
    int start, end;
    Node *left, *right;
    ll sum;
    Node(int start, int end) : start(start), end(end) {
        left = right = nullptr;
        sum = 0;
    }
    ~Node(){
        if (left) delete left;
        if (right) delete right;
    }
};

struct Segtree
{
    Node *tree;
    vector<ll> arr;
    Segtree() {
        tree = nullptr;
    }
    ~Segtree(){
        if (tree) delete tree;
    }

    void bulid(int start, int end, vector<ll> &tmp){
        arr = tmp;
        tree = init(start, end);
    }

    Node* init(int start, int end){
        Node *node = new Node(start, end);
        if (start == end){
            node->sum = arr[start-1];
            return node;
        }
        int mid = (start + end)/2;
        node->left = init(start, mid);
        node->right = init(mid+1, end);
        node->sum = node->left->sum + node->right->sum;
        return node;
    }

    void update(Node *node, int idx, int plus){
        if (node->start == node->end){
            node->sum += plus;
            return;
        }
        int mid = (node->start + node->end)/2;
        if (idx <= mid) update(node->left, idx, plus);
        else update(node->right, idx, plus);
        node->sum = node->left->sum + node->right->sum;
    }

    ll query(Node *node, int l, int r){
        if (node->end < l || r < node->start) return 0;
        if (l <= node->start && node->end <= r) return node->sum;
        int mid = (node->start + node->end)/2;
        return query(node->left, l, r) + query(node->right, l, r);
    }

};

다음 포스팅에서는 보다 최적화된 구현을 살펴보도록 하겠다.

Share on

Twitter Facebook LinkedIn

은승욱

카테고리

세그먼트 트리의 원리와 시간 복잡도

구간 합 구하기

세그먼트 트리(Segment Tree)

전처리(build)

업데이트

RSQ

시간복잡도

실제 구현

Share on

Leave a comment

You may also enjoy

edx에서 컴파일러 강의 듣기

우분투에서 클립보드 다루기

매우 빠른 입출력

백준 5373번 - 큐빙