백준 11053번 - 가장 긴 증가하는 부분 수열 - 2

가장 긴 증가하는 부분 수열 (백준 11053번)

개념 : LIS

난이도 :

링크 : LIS : https://www.acmicpc.net/problem/11053

---

이번 글에서는 $LIS$문제를 $LCS$의 일반화가 아닌, 그 자체로 다룬다.

이해를 위해 다음과 같은 배열 $A$가 있다고 가정해보자.

[9, 6, 9, 6, 1, 6, 9, 1]

그리고 손으로 직접 $A[i] \in LIS(A[1 \dots i])$를 모두 구했다고 해보자. $A[i]$를 반드시 포함하는 $LIS$ 길이임에 유의하자. 다음과 같다.

[1, 1, 2, 1, 1, 2, 3, 1]

$LIS$ 문제를 제대로 이해하기 위해 다음과 같은 그림을 그려보자.

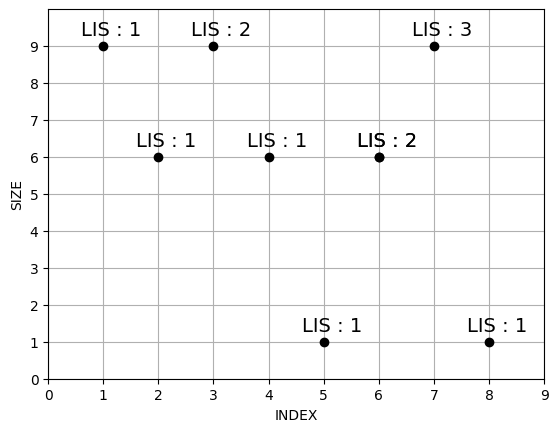
$x$축은 인덱스, $y$축은 원소의 크기이다. 이해를 위해 각 점에 $LIS(A[1 \dots i])$의 크기를 표기해두었다. 이 다음에 7원소가 들어온다고 가정해보자. 그러면 다음과 같은 영역을 생각할 수 있다.

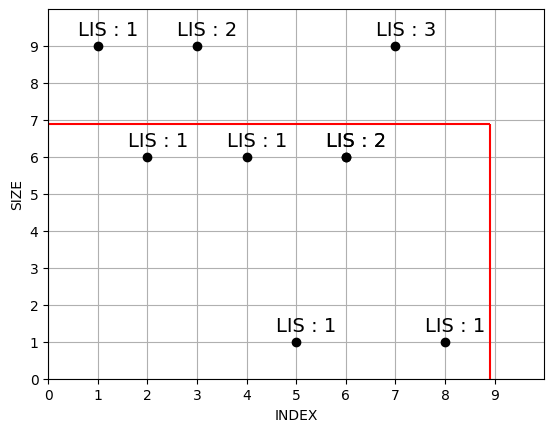
인덱스가 9보다 작고, 크기가 7보다 작은 점들이다. 이 점들 안에서 가장 $LIS$가 긴 것 다음에 7이 들어가기 때문에, 가장 긴 것 + 1이 7까지의 $LIS$가 될 것이다.

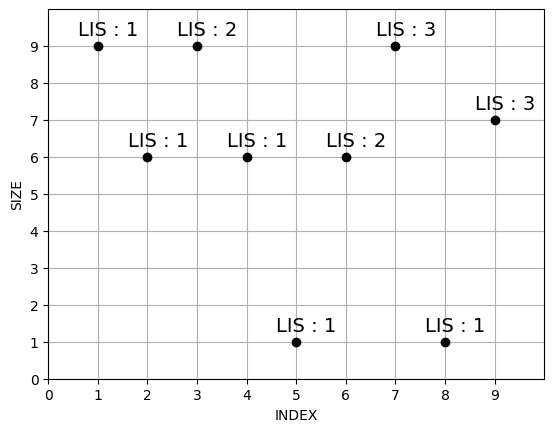
이 과정을 알고리즘으로 나타내어보자.

• $LIS(A[1 \dots i])$는 $j \in {1 \dots i-1}$, $A[i] > A[j]$인 $j$에 대해 $LIS(A[1 … j]) + 1$의 최댓값이다.

기저조건은 매우 쉬운데, 만약 그러한 $j$가 없다면 스스로 길이 1의 $LIS$를 가진다.

수식으로 나타내면 아래와 같아진다. $DP[i] = LIS(A[1 \dots i])$라고 하면 $DP$의 정의는 다음과 같다.

\[DP[i] = max_{j < i\ \cap\ A[j] < A[i]}(DP[j] + 1)\]

이를 코드로 나타내면 다음과 같아진다.

#include <bits/stdc++.h>

using namespace std;

int n;
int dp[1010];
int arr[1010];

int main() {
    cin >> n;
    for (int i=0; i<n; ++i) cin >> arr[i];
    for (int i=0; i<n; ++i) {
        dp[i] = 1;
        for (int j=0; j<i; ++j) if (arr[j] < arr[i]) {
            dp[i] = max(dp[i], dp[j] + 1);
        }
    }
    cout << *max_element(dp, dp + n);
}

단, 만약 $DP$를 다음과 같이 정의하면 좀 더 점화식이 간단해진다.

$DP[A[i]] = max_{j < i \ \cap \ A[j] < A[i]}(LIS(A[1 \dots j]))$

$LIS$문제는 수학적으로 나타내면 어렵다는 느낌을 지우기 어려운 것 같다. 쉽게 생각하면 $A[i]$가 추가되면서 $DP[A[i]]$의 값은 현재까지, $A[i]$보다 작은 값에 저장된 $LIS$중 가장 큰 값 + 1이 저장되는 것이다. 그리고 점화식은 다음과 같이 된다.

\[DP[A[i]] = max_{j<A[i]}(DP[j])\]

이를 코드로 구현하면 다음과 같다.

#include <bits/stdc++.h>

using namespace std;

int n;
int dp[1010];
int arr[1010];

int main() {
    cin >> n;
    for (int i=0; i<n; ++i) cin >> arr[i];

    for (int i=0; i<n; ++i) {
        int mx = 0;
        for (int j=0; j<arr[i]; ++j) mx = max(mx, dp[j] + 1);
        dp[arr[i]] = mx;
    }
    cout << *max_element(dp, dp + 1010);
}