백준 25954번 - LCS 9

LCS 9 (백준 25954번)

개념 : LCS

난이도 :

링크 : https://www.acmicpc.net/problem/25954

---

지금까지 LCS의 끝판왕은 bitwise를 사용하여 $O(NM/64)$에 해결하는 것이라고 생각했었다. 하지만 이번에 koosaga님의 포스트를 보고 LCS 9를 도전하기로 마음먹었고, 정말 많은 인사이트를 얻었다.

Direct Acyclic Graph (Alves, C. E. R., Cáceres, E. N., & Song, S. W. (2008). An all-substrings common subsequence algorithm. Discrete Applied Mathematics, 156(7), 1025-1035.)

히르쉬버그 알고리즘을 사용하여 LCS 문제를 최적화하는 것이 LCS 5, LCS 6, LCS 7 문제의 핵심이었다. (순서가 이상하나, LCS 5, 6, 7도 추후 다루도록 하겠다.) 히르쉬버그 알고리즘은 상태 전이를 간선으로 표현하여 DAG처럼 다루는 것이 핵심이었는데, 이 문제 역시도 그렇다.

1. 우, 하 방향으로의 상태 전이 간선의 가중치는 0이다.
2. 대각선 방향으로의 상태 전이 간선의 가중치는 1이다.

문자열 $A$와 $B$가 있고, 각각의 길이가 $N$, $M$이라면 이 두 문자열의 LCS 길이는 $(0,0) \rightarrow (N, M)$ 의 최장 거리가 된다. 이 문제에 대한 이해는 아쉽게도 koosaga님의 자료 이상으로는 해내지 못하고 있다. 따라서 처음부터 끝까지의 대한 내용은 koosaga님 블로그를 참고하기 바란다.

이 문제를 해결하기 위해 사용되는 것은 4개의 보조정리와 1개의 정리이다.

• $dist((x_1, y_1),(x_2, y_2))$ : $(x_1, y_1)$으로부터 $(x_2, y_2)$까지의 최장 거리

보조 정리 1

$dist((0, y), (i, j)) - dist((0, y), (i, j-1))$의 값은 반드시 0 또는 1이다.

아주 당연하진 않지만, 이해하기 어렵진 않다. 귀류법으로 증명 가능하다.

1. $dist((0, y), (i, j)) \le dist((0, y), (i, j-1))$

$dist((0, y), (i, j-1) > dist((0, y), (i, j))$라고 가정하면 $dist((0, y), (i, j))$의 값이 $dist((0, y), (i, j-1))$여야하므로 모순이 발생한다.

1. $dist((0, y), (i, j-1)) \ge dist((0, y), (i, j)) - 1$

$dist((0, y), (i, j-1)) < dist((0, y), (i, j)) - 1$ 라고 하면, 2 이상 차이가 나야하는데, 그렇다면 현재 이 DAG 특성상 $max_{k<=i-1}(dist((0, y), (k, j-1)))$ 값은 반드시 $dist((0, y), (i, j))-1$이어야 한다. 하지만 이 경우 수직으로 쭉 내려오기만 해도 $dist((0, y), (i, j))-1$의 값을 가지므로 모순이 발생한다.

보조 정리 2

$dist((0, y), (i, j)) - dist((0, y), (i-1, j))$의 값은 반드시 0 또는 1이다.

보조 정리 1과 완전히 같은 방식으로 증명된다.

보조 정리 3

$\forall i, j$에 대해 $0 \le i_h(i, j) \le j$ 인 $i_h(i, j)$가 존재하고, $i_h(i, j)$는 아래를 만족한다.

• $0 \le y < i_h(i, j)$인 모든 $y$에 대해 $dist((0, y), (i, j)) - dist((0,y), (i, j-1)) = 0$이다.
• $i_h(i, j) \le y < j$인 모든 $y$에 대해 $dist((0, y), (i, j)) - dist((0, y), (i, j-1)) = 1$이다.

이에 대한 증명을 생각하는 것이 가장 어려웠고, 다르게 말하면 참신했다. 우선 위 명제는 아래 명제와 동치가 된다.

$\forall y, i, j$에 대해

$dist((0, y), (i, j)) - dist((0, y), (i, j-1)) \le dist((0, y+1), (i, j)) - dist((0, y+1), (i, j-1))$ 가 성립한다.

해당 명제가 성립한다면, $dist((0, y), (i, j)) - dist((0, y), (i, j-1))$는 0과 1로만 이루어지는데, 이것이 y값에 따라 증가한다면 어느 순간에는 0에서 1로 바뀌는 y가 반드시 존재할 것이기 때문이다. 이 값이 바로 $i_h(i, j)$가 된다. (단, 존재하지 않을 수 있는데 이경우 $i_h(i, j)$가 $0$ 또는 $j$인 경우이다.) 따라서 동치인 명제를 증명한다.

해당 명제 증명을 위해 보다 편하게 수식을 변형하여 아래의 식을 증명할 것이다.

• $dist((0, y), (i, j)) + dist((0, y+1), (i, j-1)) \le dist((0, y), (i, j-1)) + dist((0, y+1), (i, j))$

그리고 이 그래프는 평면이기 때문에 반드시 $(0, y) \rightarrow (i, j)$ 최장 경로와 $(0, y+1) \rightarrow (i, j-1)$의 최장 경로는 교차할 수밖에 없다.

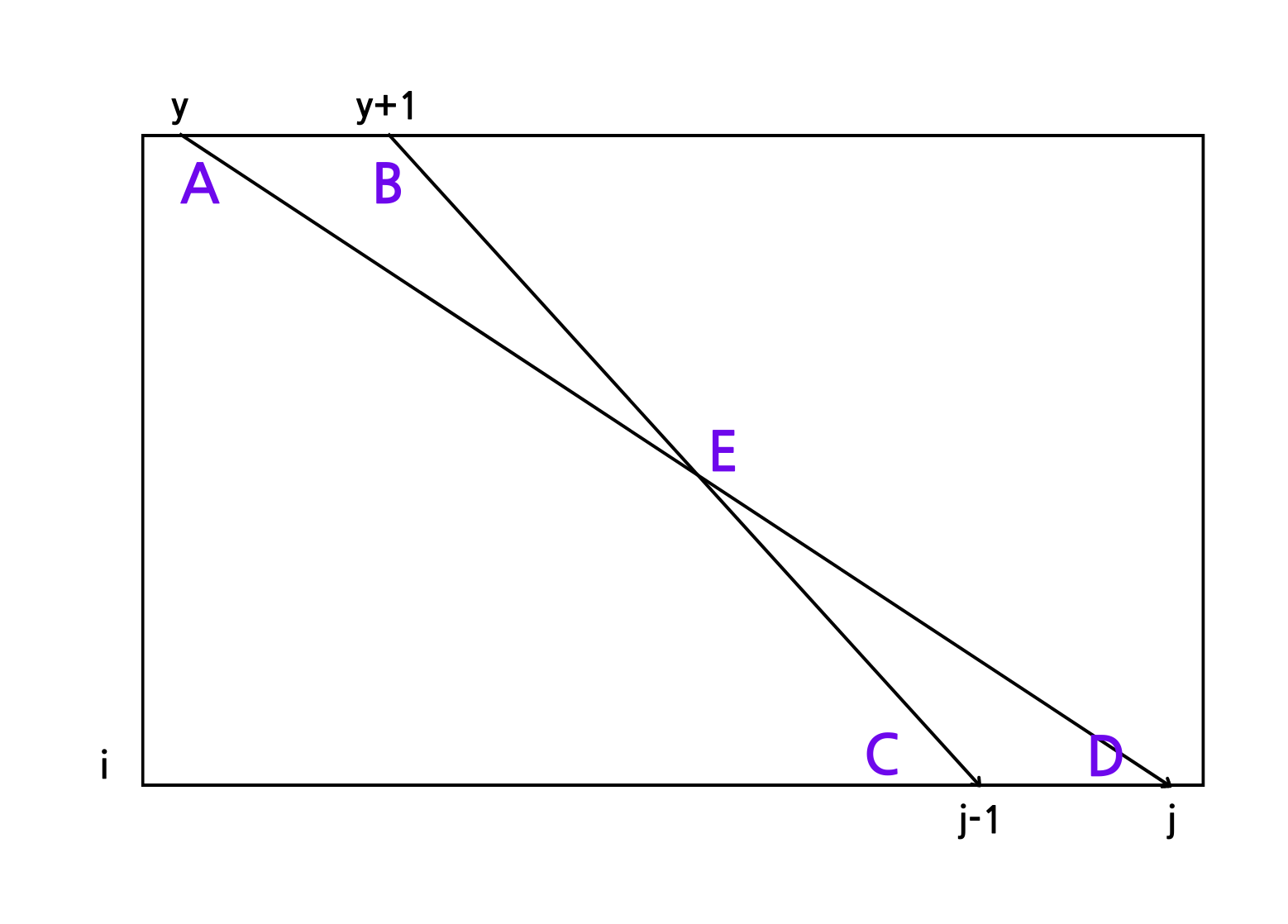
이를 간략하게 모식도로 그린 것이다. 위 그림에서 주목해야할 것은 $A \rightarrow D + B \rightarrow C$ 경로이지만 교차점으로 인해, $A \rightarrow E \rightarrow C + B \rightarrow E \rightarrow D$로도 볼 수 있다는 것이다. $A \rightarrow E \rightarrow C$ 경로는 최장 길이가 보장된 $dist((0, y), (i, j-1))$ 길이보다 작거나 같을 수 밖에 없으며, $B \rightarrow E \rightarrow D$ 경로도 $dist((0, y+1), (i, j))$보다 작거나 같을 수 밖에 없다. 따라서 위 식은 참이 될 수 밖에 없다.

보조 정리 4

$\forall i, j$에 대해 $0 \le i_v(i, j) \le j$ 인 $i_v(i, j)$가 존재하고, $i_v(i, j)$는 아래를 만족한다.

• $0 \le y < i_v(i, j)$인 모든 $y$에 대해 $dist((0, y), (i, j)) - dist((0,y), (i-1, j)) = 1$이다.
• $i_v(i, j) \le y < j$인 모든 $y$에 대해 $dist((0, y), (i, j)) - dist((0, y), (i-1, j)) = 0$이다.

보조 정리 3과 같은 방식으로 증명된다.

정리

$i_h(0,j) = j$ , $i_v(i, 0) = 0$

이는 생각해보면 자명하다. $i_h$는 $i=0$인 상태라면 항상 $dist((0, y), (0, j)) - dist((0, y), (0, j-1)) = 0$이기 때문이고, $i_v$도 같은 방식으로 설명할 수 있다.

$i, j \ge 1$, $a[i] = b[j]$ 인 경우

• $i_h(i, j) = i_v(i, j-1)$
• $i_v(i, j) = i_h(i-1, j)$

$i, j \ge 1$, $a[i] \neq b[j]$ 인 경우

• $i_h(i, j) = max(i_h(i-1, j), i_v(i, j-1))$
• $i_v(i, j) = min(i_h(i-1, j), i_v(i, j-1))$

이 증명 역시 생각하는 것이 쉽지는 않았다. 일단 이런 점화식을 생각할 수 있다는 자체도 신기하고, 또 증명을 해내는 것도 신기하다. 우선 고정된 $y$를 생각하고, $(i, j)$를 둬보자.

그러면 아래와 같은 8가지의 경우가 나올 수 있다.

• $i_h(i-1, j) \le y, \ i_v(i, j-1) < y$, $a[i] \neq b[j]$
• $i_h(i-1, j) > y, \ i_v(i, j-1) < y$, $a[i] \neq b[j]$
• $i_h(i-1, j) \le y, \ i_v(i, j-1) \ge y$, $a[i] \neq b[j]$
• $i_h(i-1, j) > y, \ i_v(i, j-1) \ge y$, $a[i] \neq b[j]$
• $i_h(i-1, j) \le y, \ i_v(i, j-1) < y$, $a[i] = b[j]$
• $i_h(i-1, j) > y, \ i_v(i, j-1) < y$, $a[i] = b[j]$
• $i_h(i-1, j) \le y, \ i_v(i, j-1) \ge y$, $a[i] = b[j]$
• $i_h(i-1, j) > y, \ i_v(i, j-1) \ge y$, $a[i] = b[j]$

8가지를 모두 글로 남기기는 무리인 것 같아 첫번째 경우만 증명해보겠다.

• $i_h(i-1, j) \le y, \ i_v(i, j-1) < y$, $a[i] \neq b[j]$

우선 $i_h(i-1, j) \le y, \ i_v(i, j-1) < y$이기 때문에 $dist((0, y), (i-1, j-1))=t$라고 한다면 아래와 같은 값이 될 것이다.

	$j-1$	$j$
$i-1$	$t$	$t+1$
$i$	$t$	$t+1$

보조 정리 3에 의하면 $j$ 방향으로 1씩 증가해야하며, 보조 정리 4에 의해면 $i$방향으로는 값이 같아야 한다. 이제 $y$값을 천천히 감소시킨다고 해보자. 감소함에 따라 $y$값은 $i_h(i-1, j), i_v(i, j-1)$ 값을 만나게 될 것이다.

• $i_h(i-1, j)$를 먼저 만날 때

	$j-1$	$j$
$i-1$	$t$	$t$
$i$	$t$	$t$

상태가 위와 같이 바뀔 것이다. 현재 $dist((0, y), (i, j)) - dist((0, y), (i, j-1))$의 값이 0이므로 $i_h(i, j) = i_h(i-1, j)$이다. $i_v(i, j)$ 값은 아직 결정되지 못한다.

• $i_v(i, j-1)$를 먼저 만날 때

	$j-1$	$j$
$i-1$	$t$	$t+1$
$i$	$t+1$	$t+1$

상태가 위와 같이 바뀔 것이다. 현재 $dist((0, y), (i, j)) - dist((0, y), (i, j-1))$의 값이 0이므로 $i_h(i, j) = i_v(i, j-1)$이다. $i_v(i, j)$ 값은 아직 결정되지 못한다.

• $i_h(i-1, j)$와 $i_v(i, j-1)$를 모두 만난 상태일 때

	$j-1$	$j$
$i-1$	$t$	$t$
$i$	$t+1$	$t+1$

$dist((0, y), (i, j)) - dist((0, y), (i-1, j)) = 1$ 드디어 0이 아니므로 $i_v(i, j)$ 값이 갱신된다. 둘 다 만나야 갱신되므로, $min(i_h(i-1, j), i_v(i, j-1))$로 갱신된다. $i_h(i, j)$의 경우 둘 중 하나라도 만나면 갱신되므로 $max(i_h(i-1, j), i_v(i, j-1))$로 갱신된다.

이러한 과정을 8개 반복하면, 위의 정리가 모두 맞아 떨어짐을 볼 수 있다.

우선 이를 LCS문제에 적용해보자. $dist((0, i), (N, j)) $

$= (dist((0, i), (N, j)) - dist((0, i), (N, j-1)))$ $ + (dist((0, i), (N, j-1))-dist((0, i), (N, j-2)))$ $ + \dots $ $ + (dist((0, i), (N, i+1)) - dist((0, i), (N, i)))$ $ + dist((0, i), (N, i))$

$ = dist((0, i), (N, i)) + \sum_{k=i+1}^j (dist((0, i), (N, k)) - dist((0, i), (N, k-1)))$ $ = 0 + \sum_{k=i+1}^j (dist((0, i), (N, k)) - dist((0, i), (N, k-1)))$

\[= \sum_{k=i+1}^j (i_h(N, k) \le i)\]

LCS 쿼리를 처리해야한다면 위 식을 이용하여 $O(NM + QlogN)$에 처리하는 것이 가능할 것이다. 하지만 우리가 풀어야하는 문제는 LCS 9이다.

잘 생각해보면 문제에서 요구하고 있는 사항은 다음과 같다.

\[\sum_{t=1}^N \sum_{i=1}^{M} \sum_{j=i}^{M} LCS(a[...t], b[i...j])\]

이를 위 공식으로 바꾸면 다음과 같다.

\[\sum_{t=1}^N \sum_{i=1}^{M} \sum_{j=i+1}^{M} \sum_{k=i+1}^j (i_h(t, k) \le i-1)\] \[= \sum_{t=1}^N \sum_{i=0}^{M-1} \sum_{j=i+1}^{M} \sum_{k=i+1}^j (i_h(t, k) \le i)\]

하지만 이 식을 봐도 도저히 시간내에 풀 수 있을 것 같지가 않다. 이제는 원소의 입장에서 생각해볼 필요가 있다.

만약 모든 $(i_h(t, k) \le i)$가 1의 값이라고 가정하고, $i$를 0, $t$를 고정시키고 생각하면 $i_h(t, k)$의 값은 다음과 같은 횟수로 정답안에 더해질 것이다. $j$를 증가시키며 포함되는 범위를 생각하면 쉽다.

k	1	2	3	4	5	…	M
	M	M-1	M-2	M-3	M-4	…	1

$i$를 증가시키면 아래와 같을 것이다.

k	1	2	3	4	5	…	M
i=0	M	M-1	M-2	M-3	M-4	…	1
i=1		M-1	M-2	M-3	M-4	…	1
i=2			M-2	M-3	M-4	…	1

이제 $i$의 값에 대해서 생각해보면 $i_h(t, k) \le i$를 만족하는 것에 대해서만 더해주어야 한다. 따라서 더해지는 값들은 아래와 같은 모습일 것이다.

k	1	2	3	4	5	…	M
i=0	M	M-1	M-2	M-3	M-4	…	1
i=1		M-1	M-2	M-3	M-4	…	1
i=2			M-2	M-3	M-4	…	1
i=3				M-3	M-4	…	1
i=4					M-4	…	1

각 피라미드의 높이는 $k$이므로 곱해지는 값은 ($(M - k + 1) \times$ (k - $i_h(t, k))$) 값이 된다.

이 모든 것을 구현한 코드는 아래와 같다.

#include <bits/stdc++.h>

using namespace std;

int iv[7070][7070];
int ih[7070][7070];
string a, b;
int n, m;


int main() {
    cin >> a >> b;
    n = a.size(); 
    m = b.size();
    for (int j=0; j<=m; ++j) ih[0][j] = j;
    for (int i=0; i<=n; ++i) iv[i][0] = 0;

    for (int i=1; i<=n; ++i) for (int j=1; j<=m; ++j) {
        if (a[i-1] == b[j-1]) {
            ih[i][j] = iv[i][j-1];
            iv[i][j] = ih[i-1][j];
        } else {
            ih[i][j] = max(ih[i-1][j], iv[i][j-1]);
            iv[i][j] = min(ih[i-1][j], iv[i][j-1]);
        }
    }

    long long ans = 0;
    for (int t=1; t<=n; ++t) for (int k=1; k<=m; ++k) {
        ans += (m - k + 1) * max(0, k - ih[t][k]);
    }
    cout << ans;
}

정말 역대급으로 어려웠고, 또 역대급으로 재밌었다. 다만 마지막 계산을 기하학적으로 해결한 것이 조금 마음에 걸린다. 좀 더 수학적으로 할 수 있는 방법이 있지 않았었을까..? 라는 생각이 계속 스친다. 다만 여기까지도 아직 쉬운 수준이라는 것이 믿기지 않는다.. Seaweed문제는 언제쯤 건드릴 수 있을지.. 잘 모르겠다.