Tags: dp, 다이나믹 프로그래밍, 백준, 알고리즘
Categories: 알고리즘
백준 18439번 - LCS 6
LCS 6 (백준 18439번)
개념 : LCS
난이도 :
링크 : LCS 6 : https://www.acmicpc.net/problem/18439
접근
이 문제의 경우 $LCS$의 길이 구하기 문제와 사실상 거의 동일하지만, 문자열의 길이가 최대 50,000으로 극단적으로 크다. 메모리 역시 제한이 8MB로 상당히 작은 편이지만, 후에 서술할 풀이에서는 크게 중요하게 작용하지는 않는다.
이전 $LCS$에서 사용한 그림을 그대로 가져와보겠다.
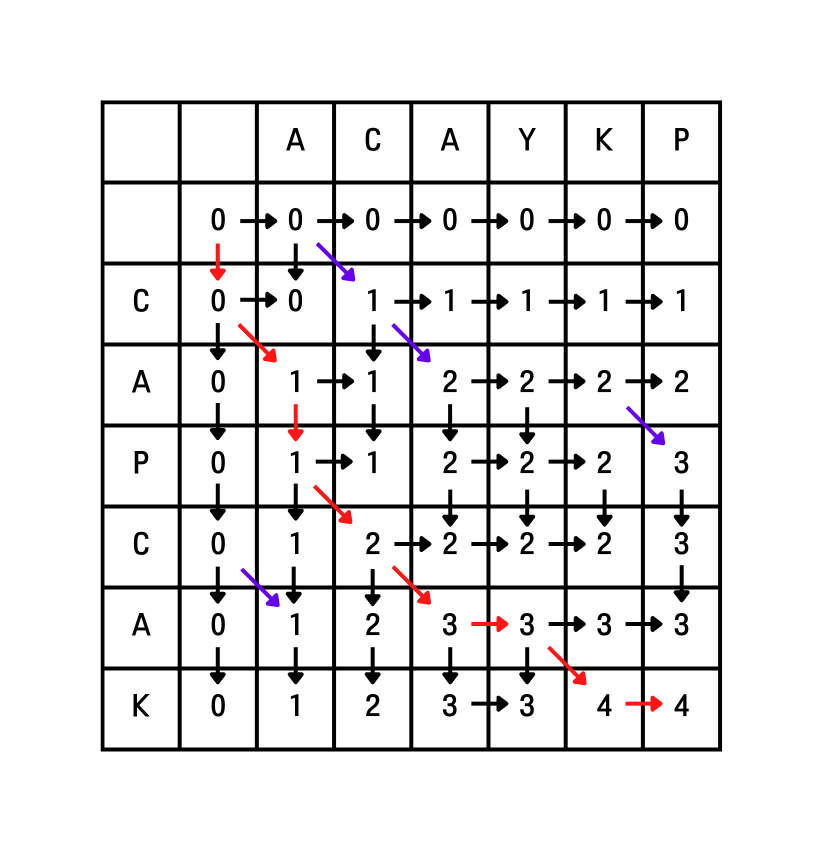
이전 $LCS 9$ 풀이에서도 서술했었으나, $DP[i][j] - DP[i][j-1]$의 값은 반드시 0 또는 1이다. 그런데 값이 0 또는 1로 표현될 수 있다는 것은 비트를 떠올리게 하지 않는가? 이제 DP테이블을 $DP[i][j] - DP[i][j-1]$로 나타내보자.
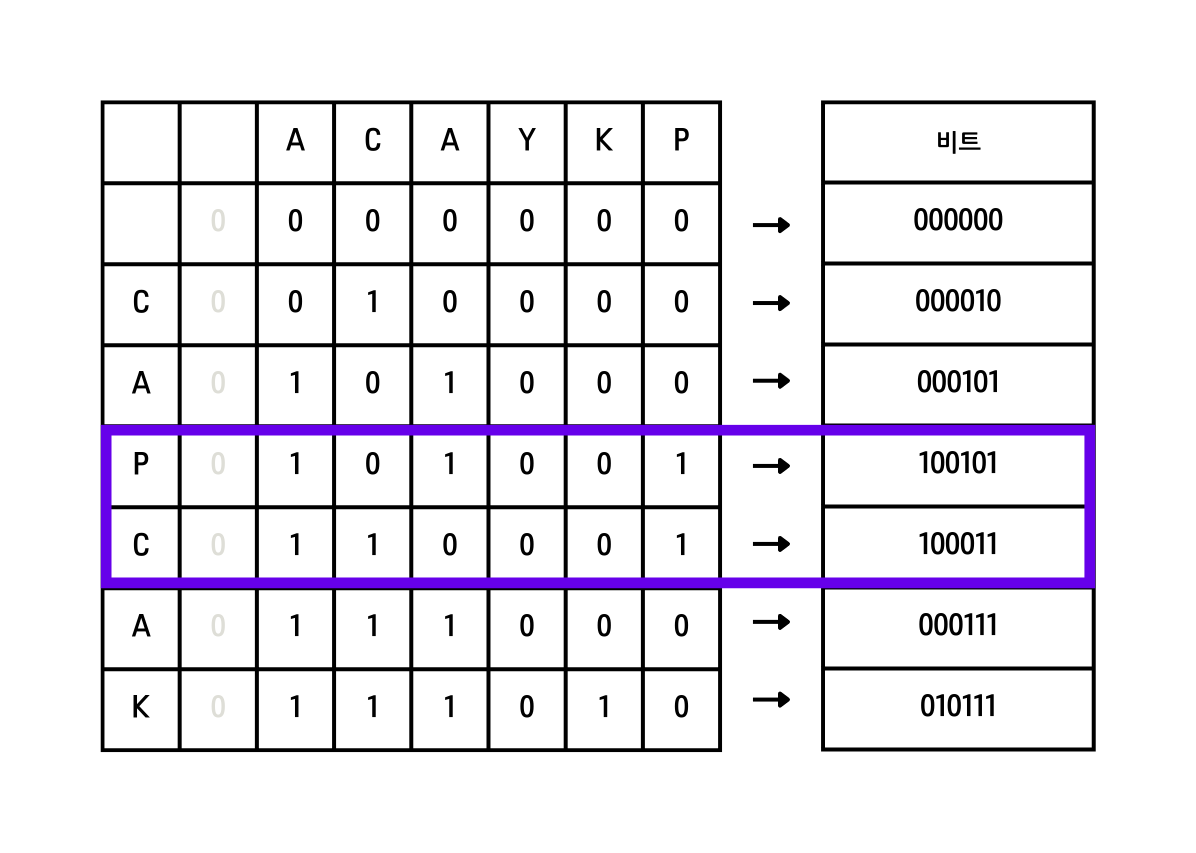
위와 같은 테이블이 만들어진다. 새롭게 만들어진 $DP$ 테이블을 $DP’$라고 정의한다. 좀 더 자세히 성질을 살펴보면 대부분의 경우 $a[i] = b[j]$를 만족하는 경우에 1이되는 것을 살펴볼 수 있으며, $i$열까지의 $LCS$ 길이는 1의 개수임을 확인할 수 있다.
비트를 이진수로 나타내면 오른쪽과 같은 수들이 될 것이다. 뒤집은 것처럼 보이지만, 배열의 $i$행의 $j$번째 원소가 $j$번째 비트와 같은 값을 갖는다. 3, 4번행인 P, C 부분을 자세히보고, 비트연산을 이용할 아이디어를 얻어보자.
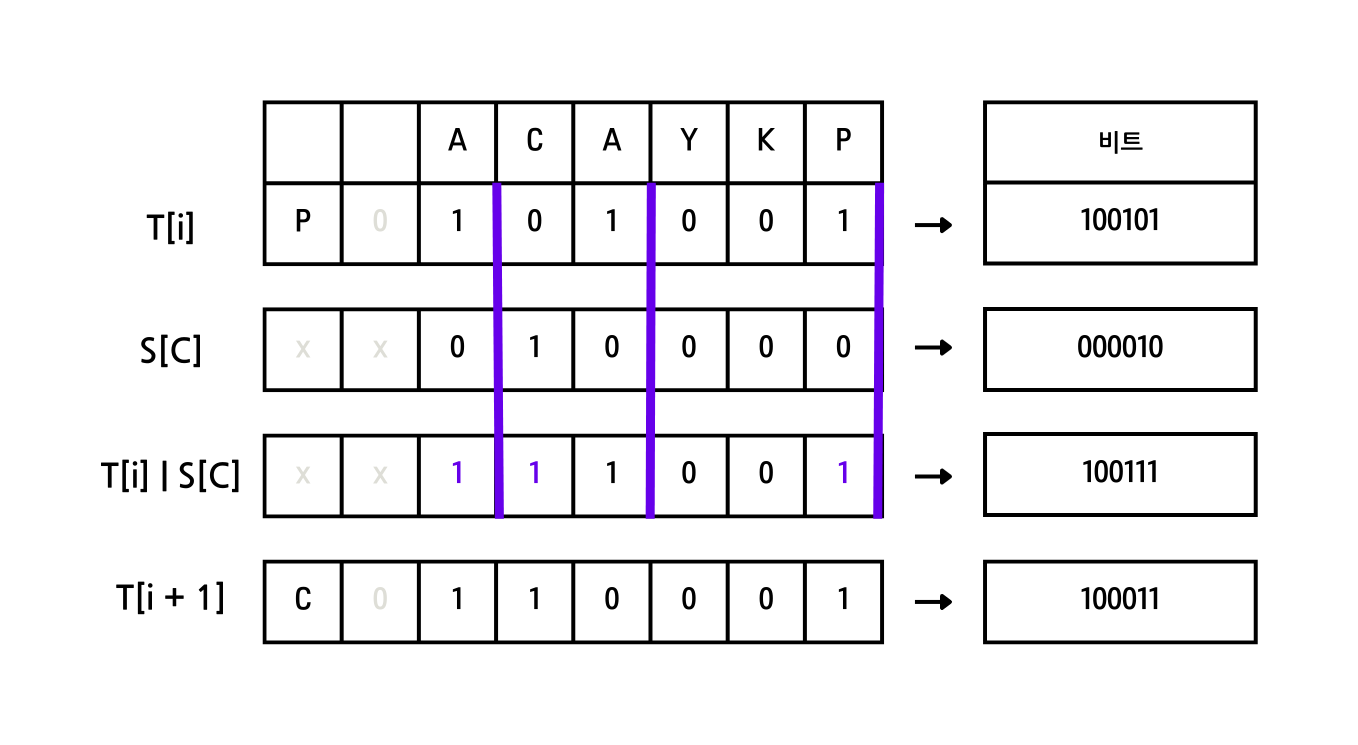
- $T[i]$ : 테이블의 $i$번째 행을 통째로 비트로 나타낸 수
- $S[X]$ : 문자열 $X = B[j]$를 만족하는 모든 $j$ 비트를 켠 수
$T[i] \rightarrow T[i+1]$ 방향의 상태전이를 위해서는 $S[X]$의 정의가 필요하다. 위 $DP’$ 테이블에서 값이 1인 곳은 $A[i] = B[j]$를 만족하는 곳들이었는데, 이를 위해 행의 문자열과 값이 같은 곳을 1로, 나머지를 0으로 하는 값이 필요한 것이다.
이제 상태전이의 규칙을 살펴보자. 우선 $DP[i][j] = 1$인 곳들을 가장 오른쪽 값으로 하는 구간들을 설정한다. $i+1$행의 문자열 $A[i+1]$은 C였으므로 $S[C]$의 값을 가져온다. $T[i+1]$의 값은 $T[i]\ | \ S[C]$ 값에서 각 구간의 최하위 비트를 켠 값과 같아진다.
정성적으로 이를 증명하면 다음과 같다.
- $DP’[i][j-1] = 1$, $DP’[i][k] = 1$,
- $DP’[i][j] = DP’[i][j+1] = \dots = DP[i][k-1] = 0$
이는 다음과 같은 모습이 될 것이다.
| $DP’$ | $\dots$ | $j-1$ | $j$ | $\dots$ | $k$ | $\dots$ |
|---|---|---|---|---|---|---|
| $i$ | $\dots$ | 1 | 0 | $\dots$ | 1 | $\dots$ |
만일 $S[A[i+1]]$가 $j, j+1, \dots k$ 구간에서 몇 개의 비트가 켜져있고, 각 열을 $e_1, e_2, \dots $라고 가정해보자. 다시 $DP’$가 아닌 $DP$로 돌아가보면 위 구간은 다음과 같은 값을 가지게 될 것이다.
| $DP$ | $\dots$ | $j-1$ | $j$ | $\dots$ | $k$ | $\dots$ |
|---|---|---|---|---|---|---|
| $i$ | $\dots$ | $a$ | $a$ | $\dots$ | $a+1$ | $\dots$ |
만일 $e_1, e_2, \dots$의 비트가 켜져있다면, 이는 곧 $A[i + 1] = B[e_i]$임을 의미한다. 따라서 $DP[i+1][e_i]$는 $DP[i][e_i-1]$에서 상태전이 한다.
$DP[i+1][e_i] = DP[i][e_i-1] + 1$ 이지만 $j - 1 \le e_i - 1 < k$ 이기 때문에 모든 $DP[i+1][e_i] = a + 1$을 만족하게 된다.
| $DP$ | $\dots$ | $j-1$ | $j$ | $\dots$ | $e_1$ | $\dots$ | $e_2$ | $\dots$ | $k$ | $\dots$ |
|---|---|---|---|---|---|---|---|---|---|---|
| $i$ | $\dots$ | $a$ | $a$ | $\dots$ | $a$ | $\dots$ | $a$ | $\dots$ | $a+1$ | $\dots$ |
| $i+1$ | $\dots$ | $a$ | $a$ | $\dots$ | $a+1$ | $\dots$ | $a+1$ | $\dots$ | $a+1$ | $\dots$ |
여기서 $DP’[i+1][j] = 1$이 되는 $j$는 $[j, k]$ 구간에서 가장 앞에서 $a+1$의 값을 가지는 $e_1$이 된다. 그리고 이 경우 $k$ 열의 값은 0이된다. 하지만 만일 위와 같은 $e_i$가 없다면, 여전히 $k$열의 값이 1을 유지해야만 한다. 따라서 $e_1, e_2, \dots e_x, k$ 중 가장 빠른 값이 이 구간에서 $DP’[i][j] = 1$을 만족한다. 이로서 $T[i] ∣ S[A[i+1]]$의 각 구간의 최하위 비트가 켜진 값이 $T[i+1]$이 됨이 증명된다.
정리
- 새로운 $DP’[i][j] = DP[i][j] - DP[i][j-1]$를 정의
- $DP’[i]$ 행을 통째로 비트로 간주한 수 $T[i]$ 정의
- $X = B[j]$를 만족하는 모든 비트를 켠 수 $S[X]$를 정의
- $T[i + 1]$는 $DP`[i][j] = 1$을 만족하는 $j$들로 구간을 나누었을 때, 각 구간에서 $T[i]\ |\ S[A[i+1]]$의 최하위 비트를 켠 수
계산
그러면 이제 이 복잡하고 어려운 수를 어떻게 구해야하는지 살펴보자. 이를 이해하기 위해 필수적인 것이 특정 수의 최하위 비트를 켜는 것이다.
68 = 01000100
68-1 = 01000011
~(68-1) = 10111100
68 & ~(68-1) = 00000100
특정 수의 최하위 비트만 켜는 것은 X & ~(X - 1) 연산으로 할 수 있다. (이는 사실 X & -X와 같다.) 그러나 이를 다른 관점에서 보면 전체 구간에서 가장 작은 비트를 켠 값, 즉 0번 비트를 켠 값인 1로 빼주고, not, & 한 것으로 생각할 수 있다. 이는 위 $T[i]$의 각 구간의 가장 작은 비트를 킨 값만 얻을 수 있다면 간단한 연산을 통해 $T[i+1]$의 값을 얻을 수 있음을 시사한다. 그리고 이는 생각 이상으로 매우 쉽다.
T[i] = 01001100
S[A[i+1]] = 00101001
T[i] | S[A[i+1]] = 01101101
위와 같다고 한다면 다음과 같이 구간을 나눌 수 있다.
T[i] = 0|100|1|100
S[A[i+1]] = 0|010|1|001
T[i] | S[A[i+1]] = 0|110|1|101
현재는 비트연산으로, 이진수를 다루고 있기 때문에 경계의 방향이 1의 왼쪽임에 주의하자. 여기서 $T[i]$를 1비트 왼쪽으로 이동하고, 0번 비트를 켜면 다음과 같다.
T[i] = 0|100|1|100
T[i] << 1 | 1 = 1|001|1|001
S[A[i+1]] = 0|010|1|001
T[i] | S[A[i+1]] = 0|110|1|101
비트를 한칸 움직임으로써, 가장 큰 비트가 다음 구간의 가장 작은 비트가 되었으며, 0번 비트를 켜줌으로써 가장 작은 구간의 가장 작은 비트 역시 켜진 것을 볼 수 있다.
T[i] << 1 | 1 = 1|001|1|001
T[i] | S[A[i+1]] = 0|110|1|101
각 구간의 가장 작은 값이 켜졌으므로 이제 간단한 연산만으로 구할 수 있다. $X = T[i] \ | \ S[A[i+1]]$라고 하고, $Y = T[i] « 1 \ |\ 1$라고 하자. 위에서 최하위 비트를 켜주었던 것 처럼 X & ~(X - Y)만 해주면 $T[i + 1]$의 값을 구할 수 있다.
X = 0|110|1|101
Y = 1|001|1|001
X - Y = 1|101|0|100
~(X - Y) = 0|010|1|011
X & ~(X - Y) = 0|010|1|001 ( = T[i + 1])
계산 방법
그러나 이제 문제가 남아있으니, 바로 비트의 길이가 50,000이나 되어야한다는 점인데, $2^{50000}$ 크기의 정수를 저장할 컴퓨터가 있으리 만무하니 다른 방법을 해결해야만 한다. 여기서 bitset이 등장한다. C++에는 이미 bitset 라이브러리를 제공하고 있으나, 아쉽게도 뺄셈 연산이 정의되어있지 않아 직접 bitset 을 구현해야 한다.
이건 어쩔 수 없이 빡세게 구현해야 한다. 64비트 unsigned long long으로 대략 800개의 배열을 채우면 50,000개의 비트를 만들 수 있다. 이후 <<, -, ~ 연산을 오버로딩하여 구현하자. 나는 비교적 구현이 쉬운 + 연산을 구현 후 A - B = A + (~B + 1)임을 이용하여 뺄셈을 구현하였다. 단, 느리기 때문에 직점 뺄셈을 구현하는 편이 더 속도면에서는 유리하다.
아래는 전체 코드이다.
#include <bits/stdc++.h>
#define all(v) v.begin(), v.end()
using namespace std;
struct bset {
#define WORD 64
#define TABLE_SIZE 800
using word = uint64_t;
word table[TABLE_SIZE];
bset() {
memset(table, 0, sizeof(table));
}
bset(word x) {
memset(table, 0, sizeof(table));
table[0] = x;
}
bool operator[](int i) {
int j = i % WORD;
i /= WORD;
return table[i] >> j & 1;
}
void set(int i, int v) {
int j = i % WORD;
i /= WORD;
if (v) table[i] |= ((word)1 << j);
else table[i] &= ~((word)1 << j);
}
bset operator+(const bset &other) const {
bset ret;
word carry = 0;
for (int i=0; i<TABLE_SIZE; ++i) {
ret.table[i] = table[i] + carry;
carry = 0;
if (table[i] > ret.table[i]) carry = 1;
ret.table[i] += other.table[i];
if (other.table[i] > ret.table[i]) carry = 1;
}
return ret;
}
bset operator+(int v) const {
bset tmp(v);
return (*this) + tmp;
}
bset operator~() const {
bset ret;
for (int i=0; i<TABLE_SIZE; ++i) {
ret.table[i] = ~table[i];
}
return ret;
}
bset operator&(const bset &other) const {
bset ret;
for (int i=0; i<TABLE_SIZE; ++i) {
ret.table[i] = table[i] & other.table[i];
}
return ret;
}
bset operator|(const bset &other) const {
bset ret;
for (int i=0; i<TABLE_SIZE; ++i) {
ret.table[i] = table[i] | other.table[i];
}
return ret;
}
bset operator|(int v) const {
bset tmp(v);
return (*this) | tmp;
}
bset operator-(const bset &other) const {
return (*this) + (~other + 1);
}
bset operator-(int v) const {
bset tmp(v);
return (*this) - tmp;
}
bset operator<<(int i) {
bset ret;
for (int j=0; j<TABLE_SIZE; ++j) {
ret.table[j] = table[j] << i;
if (j) ret.table[j] |= table[j-1] >> (WORD - i);
}
return ret;
}
#undef WORD
#undef TABLE_SIZE
};
string a, b;
int n, m;
bset A[26];
int main() {
cin >> a >> b;
if (a.size() > b.size()) swap(a, b);
n = a.size(), m = b.size();
for (int j=0; j<m; ++j) {
A[b[j] - 'A'].set(j, 1);
}
bset B;
for (int i=0; i<n; ++i) {
bset X = B | A[a[i] - 'A'];
bset Y = B << 1 | 1;
B = X & ~(X - Y);
}
int ans = 0;
for (int i=0; i<m; ++i) ans += B[i];
cout << ans;
}
시간복잡도
bitset의 모든 연산은 $O({M \over 64})$ 만큼 소요된다. $N$번 반복하여 구하기 때문에 $O({NM \over 64})$만큼 소요된다. 50,000을 넣고 계산해도 대략 넉넉하게 풀릴 정도가 된다.
풀어보면 좋은 연습문제
위 LCS를 구하는 것을 함수로 만들어서 구현하면 끝
시간이 빡세서.. bitset 라이브러리에서 뺄셈 연산을 정의하면 할 수 있다. 혹은 $LCS \ 9$ 풀이로 풀 수 있다.
$Y$는 양쪽 문자열에서 전부 제거하고 $X$ 를 기준으로 $A_1, A_2$, $B_1, B_2$로 분리한뒤 $LCS(A_1, B_1) + 1 + LCS(A_2, B_2)$를 구하면 끝.


Leave a comment