백준 13711번 - LCS 4

LCS 4 (백준 13711번)

개념 : LIS

난이도 :

링크 : LCS 4 : https://www.acmicpc.net/problem/13711

---

접근

$LCS$와 $LIS$ 포스팅에 대해 미리 공부하고 오기를 추천한다.

LCS 1, 2

LIS

해당 문제의 $N$의 크기는 무려 100,000이다. 우리가 배운 $LCS$ 알고리즘은 $O(NM)$의 시간을 소요하기 때문에, $LCS$ 알고리즘은 활용할 수 없다. 이 문제에 한해서는 $LIS$를 활용할 수 있다.

1부터 N까지 정수가 모두 한 번씩 등장하는 두 수열 A와 B가 주어졌을 때라는 문구가 주어진 것이 매우 큰 힌트이다. 중복되는 수가 없기 때문에, 두 수열의 같은 수는 1:1로 매치하는 것이 가능하다.

우선 두 배열이 다음과 같다고 해보자.

[7, 3, 8, 4, 2, 6, 10, 1, 5, 9]
[9, 4, 5, 3, 10, 6, 1, 8, 7, 2]

이를 그림으로 그려보면 다음과 같다.

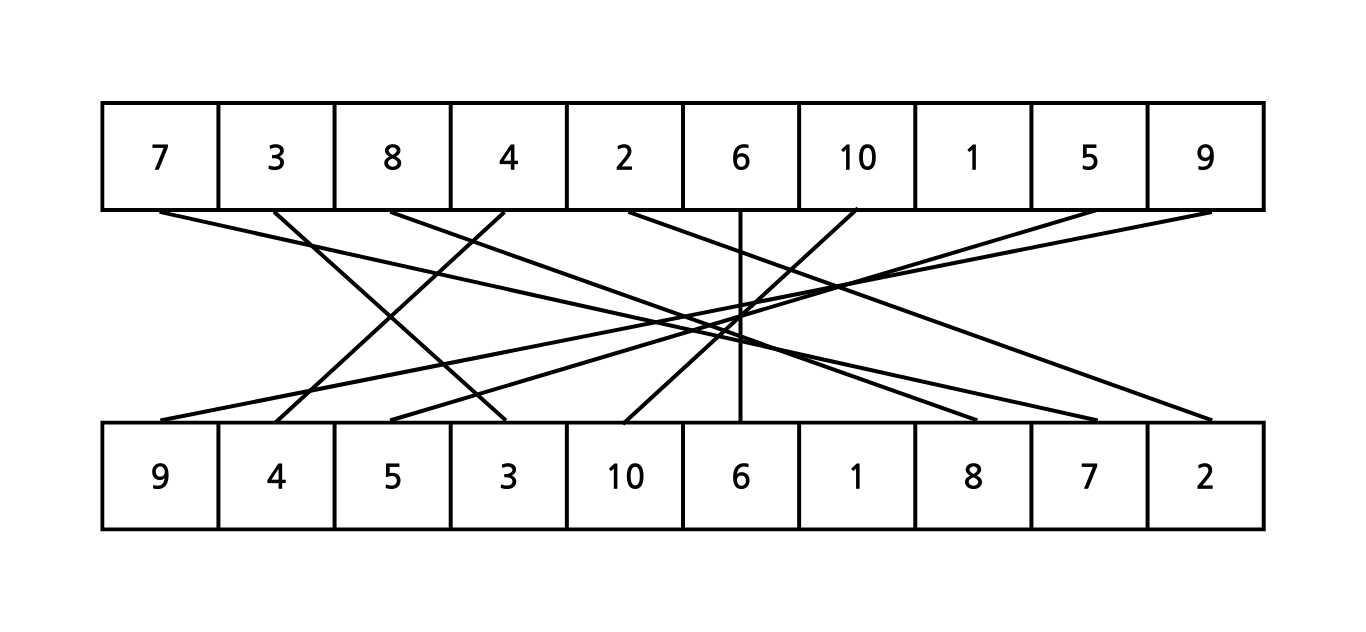
이 중 가장 긴 공통 부분 문자열은 교차하지 않는 가장 큰(많은) 선분 집합의 크기가 된다.

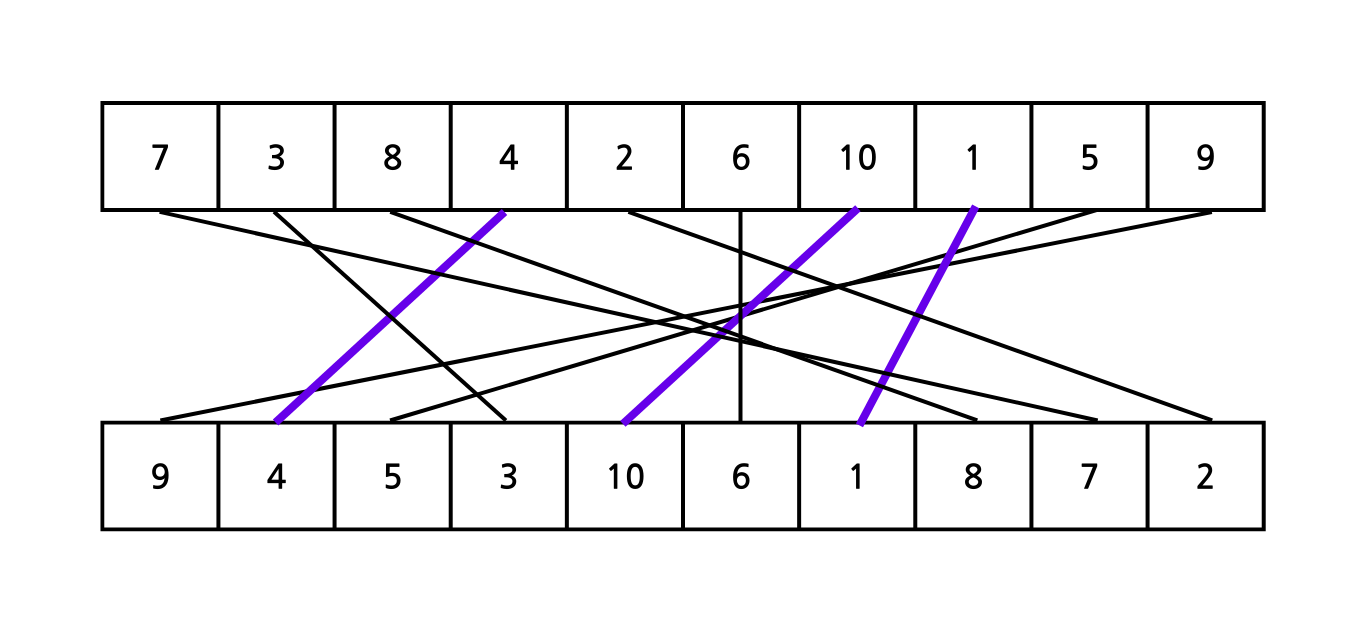
보라색으로 표시된 것은 그 중 하나이다. 각각의 수는 1:1로 대응되기 때문에, 배열 하나를 index로 리넘버링하고, 다른 배열 하나도 대응된 index로 바꿔주어도 상관이 없다.

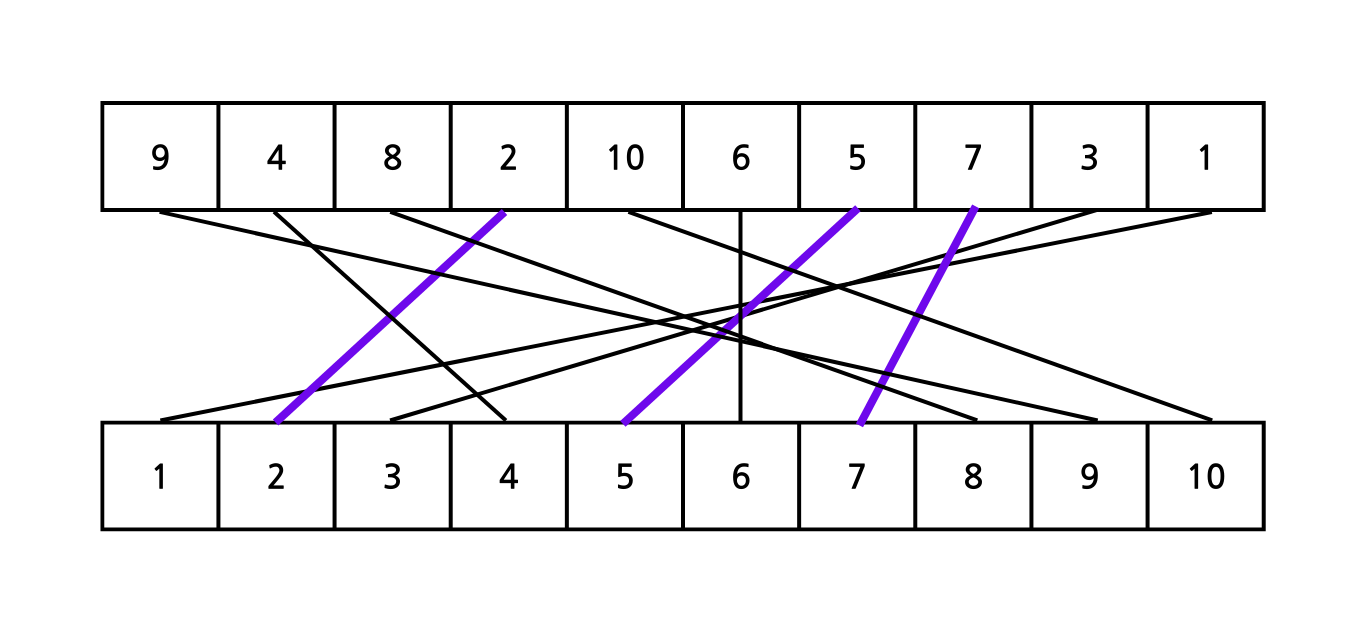
두 번째 배열을 리넘버링해주었다. $LIS$의 첫 번째 풀이를 기억한다면 위 문제는 더 이상 $LCS$가 아닌 $LIS$문제로 환원됨을 알 수 있을 것이다. 따라서 문제는 $O(NlogN)$으로 해결된다.

아래는 코드이다.

#include <bits/stdc++.h>
#define MAX 1'010'101'010

using namespace std;

int n;
int A[101010], B[101010];
int rev[101010];
int lis[101010];

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    cin >> n;
    for (int i=0; i<n; ++i) {
        cin >> A[i];
        rev[A[i]] = i;
    } 
    for (int i=0; i<n; ++i) {
        cin >> B[i];
        B[i] = rev[B[i]];
    } 

    fill(lis, lis + n + 1, MAX);
    for (int i=0; i<n; ++i) {
        int f = lower_bound(lis, lis + n + 1, B[i]) - lis;
        lis[f] = min(lis[f], B[i]);
    }
    int ans = 0;
    while (lis[ans] != MAX) ans++;
    cout << ans;
}

같이 풀어볼만한 문제들

• 꼬인 전깃줄
• 전깃줄 2