백준 9251, 9252번 - LCS 1, 2

LCS, LCS 2 (백준 9251, 9252번)

개념 : LCS

난이도 :

링크 : LCS : https://www.acmicpc.net/problem/9251 LCS 2 : https://www.acmicpc.net/problem/9252

---

LCS(Longest Common Subsequance)는 대표적인 DP 문제로 편집 거리 문제와 함께, 문자열 DP를 대표하는 문제 중 하나이다. 문제의 요점은 아래와 같다.

두 문자열이 공통으로 갖는 부분 문자열 중 가장 긴 것을 구하라

문자열의 길이를 $N$이라고 하자. 문자열에서 0개 이상, $N$개 미만의 문자를 빼내고 남은 문자열을 부분 문자열이라고 볼 수 있다.

''' "abcd"의 부분 문자열 '''

'a', 'b', 'c', 'd', 'ab', 'ac', 'ad', 'bc', 'bd', 'cd', 'abc', \
'abd', 'acd', 'bcd', 'abcd'

두 문자열의 길이는 최대 1000글자이기 때문에 나이브한 풀이는 절대 통과할 수 없다. DP로 해결해보자.

문자열 $A$, $B$의 길이를 각각 $N$, $M$이라고 하면 다음이 성립한다는 것을 알 수 있다.

경우 1. $A[n] \neq B[m]$

$A[1 \dots n], B[1 \dots m]$의 $LCS$로 가능한 것은 두 가지 경우이다.

1. $A[1 \dots n-1], B[1 \dots m]$의 $LCS$
2. $A[1 \dots n], B[1 \dots m-1]$의 $LCS$

각각의 경우 문자열 하나를 붙인다고 해도, $A[n]$과 $B[m]$이 다르기 때문에 $LCS$의 길이는 늘어나지 않는다. 따라서 두 $LCS$ 중에서 큰 값을 고르면 된다.

경우 2. $A[n] = B[m]$

이 경우 $A[1 \dots n],B[1 \dots m]$의 $LCS$로 가능한 것은 한가지 밖에 없다.

• $A[1 \dots n-1], B[1 \dots m-1]$의 $LCS$ $+ 1$

$A[1 \dots n-1], B[1 \dots m]$의 $LCS$와 $A[1 \dots n], B[1 \dots m-1]$의 $LCS$는 어차피 $A[1 \dots n-1], B[1 \dots m-1]$의 $LCS$의 값과 1 이하의 차이밖에 나지 않으므로 고려할 필요가 없다.

이제 $DP$를 다음과 같이 정의해보자.

\[DP[i][j] = LCS(A[1 \dots i], B[1 \dots j])\]

이제 다음과 같은 점화식을 만들 수 있다.

1. $A[i] \neq B[j]$

\[DP[i][j] = max(DP[i-1][j], DP[i][j-1])\]

1. $A[i] = B[j]$

\[DP[i][j] = DP[i-1][j-1] + 1\]

동적 계획법에서 가장 중요한 상태 전이가 정의되었으니, 기저 조건을 파악해보자. 빈 문자열 역시 문자열이라고 정의한다면 다음과 같은 기저조건을 얻을 수 있을 것이다.

\[DP[0][j] = LCS(A[1 \dots 0], B[1 \dots j]) = 0\] \[DP[i][0] = LCS(A[1 \dots i], B[1 \dots 0]) = 0\]

그리고 $i$ 또는 $j$가 $0$인 상황에서 다음 $DP$값으로 상태 전이하는 것 역시 큰 문제가 없다.

• $i = 0, j = 0 \rightarrow i=1, j=1$
• $i = 0, j \neq 0 \rightarrow i=1, j \neq 0$
• $i \neq 0, j = 0 \rightarrow i \neq 0, j = 1$

3가지 상황에 대해 모두 정상적으로 상태 전이가 되는지 확인만 하면 될 것이다.

정리하면 다음과 같다.

• $DP[i][0] = DP[j][0] = 0$
• $DP[i][j] = max(DP[i-1][j], DP[i][j-1]) $
• $DP[i][j] = DP[i-1][j-1] + 1$

이제 이 점화식을 코드로 작성하면 다음과 같다.

#include <bits/stdc++.h>

using namespace std;

int dp[1010][1010];
int n, m;
string a, b;

int main() {
    cin >> a >> b;
    n = a.size();
    m = b.size();
    for (int i=1; i<=n; ++i) for (int j=1; j<=m; ++j) {
        if (a[i-1] == b[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
        else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
    }
    cout << dp[n][m];
}

역추적

$LCS$를 직접 구하기 위해서는 위 상태 전이 그래프에 대해 이해할 필요가 있다. $(0,0)$에서 $(N, M)$에 이르는 길을 구하기만 하면 된다. 이러한 길은 여러 개가 있을 수 있으며, LCS2 문제를 해결하기 위해서는 이 중 1개만 구하면 된다. $(0, 0)$에서 $(N, M)$까지 top-down 방식으로 간선을 구해도 되지만, 이는 $O(NM)$의 시간이 소요되므로 역추적 방식을 이용하자. 이를 이용하면 $O(N + M)$ 시간에 $LCS$를 구할 수 있다.

역추적은 $(N, M)$에서 시작하여 $(0, 0)$을 찾아 거꾸로 진행한다. 다음과 같은 알고리즘을 사용하면 반드시 1개를 구할 수 있다.

현재 좌표를 $(i, j)$라고 하자.

1. $A[i] = B[j]$라면 결과물에 $A[i]$를 추가하고 $(i-1, j-1)$로 이동
2. $dp[i][j] = dp[i][j-1]$ 라면 $(i, j-1)$로 이동
3. $dp[i][j] = dp[i-1][j]$라면 $(i-1, j)$로 이동

대각선 방향의 간선을 최우선으로 찾고 그 외의 경로는 상태전이가 가능한 방향으로 이동하는 것이다. 마지막으로 기록한 결과물을 거꾸로 뒤집으면 $LCS$가 된다. 아래는 위 알고리즘으로 구한 경로이다.

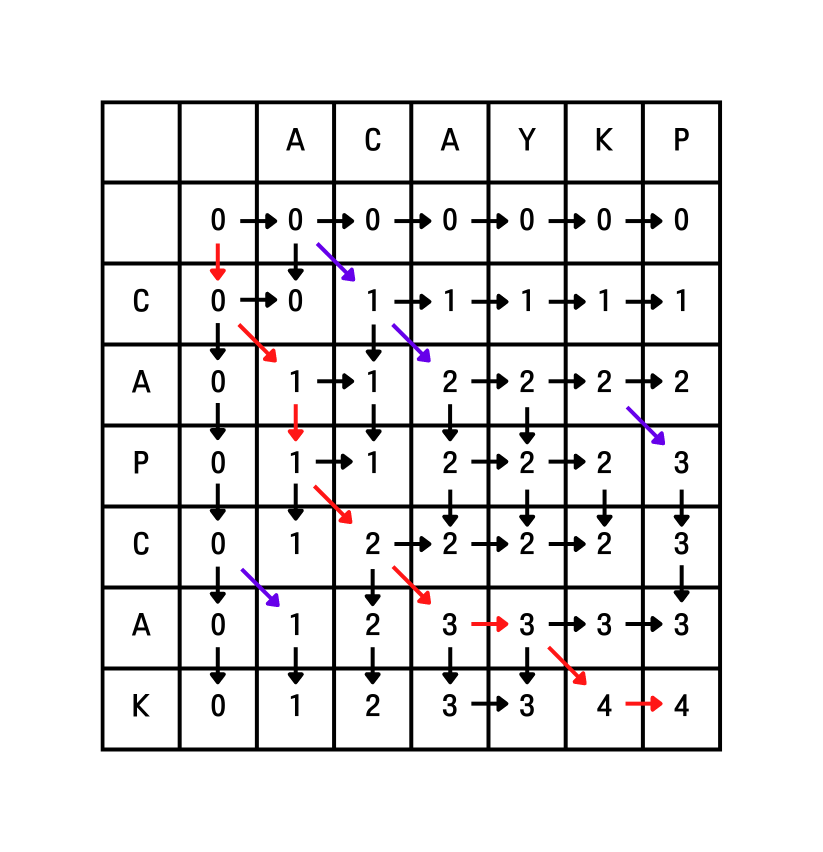
이제 이것을 코드로 구현해보자.

#include <bits/stdc++.h>

using namespace std;

int dp[1010][1010];
int n, m;
string a, b;
string ans;

int main() {
    cin >> a >> b;
    n = a.size();
    m = b.size();
    for (int i=1; i<=n; ++i) for (int j=1; j<=m; ++j) {
        if (a[i-1] == b[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
        else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
    }

    for (int i=n, j=m; i!=0 || j!=0; ) {
        if (i && j && a[i-1] == b[j-1]) {
            ans += a[i-1];
            i--, j--;
        } else if (j && dp[i][j] == dp[i][j-1]) j--; 
        else i--;
    }
    reverse(ans.begin(), ans.end());
    cout << ans.size() << '\n' << ans;
}

$O(NM + N + M)$ 시간 안에 모든 LCS2 문제까지 해결하는 것이 가능하다. 추가적으로 LCS 3 문제의 경우 해당 문제의 일반화이기 때문에, 따로 포스팅은 하지 않을 예정이다.